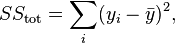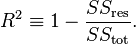예측(모델)이 얼마나 현상을 잘 설명하는지에 대한 척도로써 우린 R² 값을 주로 사용한다.

다음은  위키피디아의 설명이다. https://en.wikipedia.org/wiki/Coefficient_of_determination

A data set has n values marked y₁...y_n (collectively known as y_i), each associated with a predicted (or modeled) value f₁...f_n (known as f_i, or sometimes ŷ_i).

If is the mean of the observed data:

then the variability of the data set can be measured using three sums of squares formulas:

• The total sum of squares (proportional to the variance of the data):

• The regression sum of squares, also called the explained sum of squares:

• The sum of squares of residuals, also called the residual sum of squares:

The most general definition of the coefficient of determination is

자 수식은 간단하게 설명되었다.

관측값의 평균

각 관측값과 관측값의 평균과의 편차의 제곱들의 합

각 예측값과 관측값의 평균과의 편차의 제곱들의 합,

각 관측값과 각 예측값에 대한 편차의 제곱들의 합,

그 중 SSres와 SStot 만을 사용하면 R²을 구할 수 있다.

global_m 모듈에 get_average() 함수로 평균을 구하는 함수로.. sp, dp도 선언되어있음..

sp용 dp용을 만들어 제네릭 프로그래밍

module regression_m
    use :: global_m
    implicit none

    interface rsquare
        module procedure rsquare_sp, rsquare_dp
    end interface

contains

    pure function rsquare_sp (y, f) result (rsquared)
        real(kind=sp), intent(in   ) :: y(:), f(:)
        real(kind=sp) :: rsquared, ssres, sstot, ym

        ym = get_average(y)
        sstot = sum((y - ym)**2)
        ssres = sum((y - f)**2)

        rsquared = 1.0_sp - (ssres/sstot)

    end function 

    pure function rsquare_dp (y, f) result (rsquared)
        real(kind=dp), intent(in   ) :: y(:), f(:)
        real(kind=dp) :: rsquared, ssres, sstot, ym

        ym = get_average(y)
        sstot = sum((y - ym)**2)
        ssres = sum((y - f)**2)

        rsquared = 1.0_dp - (ssres/sstot)

    end function
    
end module